分析负数取模与取余的规则

负数"取模"

基本概念

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r,且0 <= r < d。其中，q 被称为商，r 被称为余数。

//对应代码

int main()
{
int a = 10;
int d = 3;
printf("%d\n", a % d); //结果是1
//因为：a=10,d=3,q=3,r=1 0<=r<d(3)
//所以：a = q*d+r -> 10=3'3+1

return 0;

}

正数比较简单,我们不谈,只看负数,负数的情况还是比较复杂的,先来看看不同平台下负数"取模"的差异

int main()
{
    int a = -10; 
    int d = 3;
    printf("%d\n", a/d); 
    printf("%d\n", a%d);
}

可以看出不同平台下C语言"取模"和取商是没有区别的.再看看python环境下的.

centos7默认python版本是2.7.5,故使用python 2.7.5版本测试. 也可以使用python3.7.3版本测试,结果是相同的

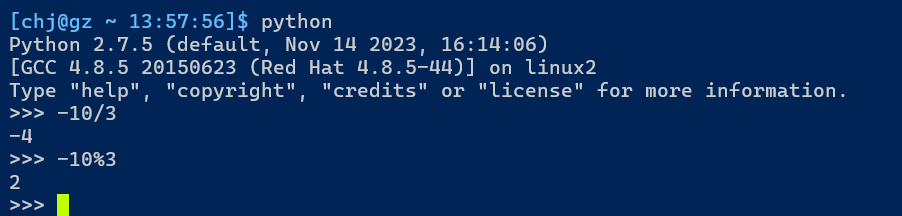
可以发现两种语言负数求商和取余结果是不一样的.

定义中规定,余数是要大于等于0的,而C语言却计算出了负数.

结论:很显然,上面关于取模的定义,并不能满足语言上的取模运算.

因此引出了修正定义

修正定义

因为在C中，-10%3出现了负数，根据定义：满足 a = q*d + r 且0 <= r < d，C语言中的余数，是不满足定义的，因为，r<0了。
故，大家对取模有了一个修订版的定义：
如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 <= |r| < |d|。其中，q 被称为商，r 被称为余数。
有了这个新的定义，那么C中或者Python中的“取模”，就都能解释了。
解释C: -10 = (-3) ' 3 + (-1)
解释Python：-10 = （?）' 3 + 2,其中，可以推导出来,'?'必须是-4(至于为什么,后面验证),即-10 = （-4）' 3 + 2，才能 满足定义。
所以，在不同语言，同一个计算表达式，负数“取模”结果是不同的。我们可以称之为分别叫做正余数 和 负余数

是什么决定了这种现象?

具体余数r的大小,本质是取决于商的,商确定了,余数自然就能确定.

而商取决于什么? 答案是,取决于除法计算的时候,结果的取整规则.

取整规则决定商的值

C语言中取整规则默认是向0取整,python中默认取整规则是向下取整.

根据它们两个的规则,显然大于0的情况都是相同的,而小于0的情况是不同的,因此负数的情况下的它们的结果不相同

因为它们两的取整规则不同,而且又必须满足修订版的"取模"规则,决定了它们的计算结果现象

还有一个问题,那就是既然不同语言%符号计算的值不一样,那还是模数或余数吗?或者说取余和取模一样吗?

取模和取余不一样.

定义

取余：尽可能让商，进行向0取整. //即零向取整方式得到的是余数

取模：尽可能让商，向-∞方向取整. //即向下取整方式得到的是模数
//模数,在几何向量上看,模是长度,为正值.(不考虑复数).模是正是负具体还要结合相关领域的定义.在计算机科学中,模和余很多情况是不区分的.

根据定义:

C中%运算,本质是取余数.

python中%运算,本质是取模.

再根据取整规则来看:

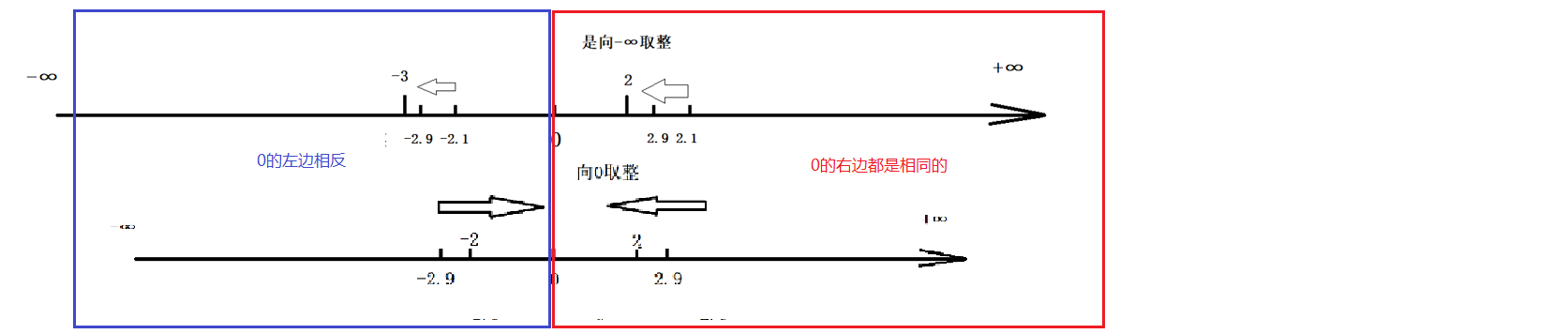
对任何一个大于0的数，对其进行0向取整和-∞取整，取整方向是一致的。故取模等价于取余
对任何一个小于0的数，对其进行0向取整和-∞取整，取整方向是相反的。故取模不等价于取余

小归纳:

同符号数据相除，得到的商，根据数学同符号相消规则,一定是正数，即大于0！ 大于0取整方式就是相同的.
故，在对其商进行取整的时候，取模等价于取余。